Specific heat capacity, also known simply as specific heat, is the measure of the heat energy required to increase the temperature of a unit quantity of a substance by a certain temperature interval. The term originated primarily through the work of Scottish physicist Joseph Black who conducted various heat measurements and used the phrase "capacity for heat.".

Basic metrics of specific heat capacity
When measuring specific heat capacity in science and engineering, the unit quantity of a substance is often in terms of mass: either the gram or kilogram, both of which are an SI unit. Especially in chemistry though, the unit quantity of specific heat capacity may also be the mole, which is a certain number of molecules or atoms. When the unit quantity is the mole, the term molar heat capacity may also be used to more explicitly describe the measure.

Unit quantity
The unit of measure for heat energy is usually the SI unit joule. The calorie however, is still often used in chemistry.

Heat energy
The temperature interval in science, engineering, and chemistry is usually one kelvin or degree Celsius (both of which have the same magnitude).

Temperature interval
In the U.S., other units of measure for specific heat capacity are typically used in disciplines such as construction and civil engineering. There, the mass quantity is often the pound-mass, the unit of heat energy is the British thermal unit, and the temperature interval is the degree Fahrenheit.

Other units

Q = m c ΔT
where Q is the heat energy put into or taken out of the substance, m is the mass of the substance, c is the specific heat capacity, and ΔT is the temperature differential.

Q = n C ΔT
where Q is the heat energy put into or taken out of the substance, n is the number of moles, C is the specific heat capacity, and ΔT is the temperature differential.

The equation relating heat energy to specific heat capacity, where the unit quantity is in terms of mass is:
Where the unit quantity is in terms of moles, the equation relating heat energy to specific heat capacity (also known as molar heat capacity) is Basic equations
Since Factors that affect specific heat capacity
When mass is the unit quantity, the symbol for specific heat capacity is lowercase c. When the mole is the unit quantity, the symbol is uppercase C. Alternatively—especially in chemistry as opposed to engineering—the uppercase version for specific heat, C, may be used in combination with a suffix representing enthalpy (symbol: either H or h); specifically, when the mole is the unit quantity, the enthalpy suffix is uppercase H and when mass is the unit quantity, the suffix is lowercase h.
The modern SI units for measuring specific heat capacity are either the joule per gram-kelvin (J g (100 °C, 101.325 kPa)
Note in the above specification that the experimental condition is at constant volume. Still, the pressure within this fixed volume is controlled and specified.

Heat capacity
Assuming an altitude of 194 meters above mean sea level (the world–wide median altitude of human habitation), an indoor temperature of 23 °C, a dewpoint of 9 °C (40.85% relative humidity), and 760 mm–Hg sea level–corrected barometric pressure (molar water vapor content = 1.16%).

Table of specific heat capacities
(Usually of interest to builders and solar designers)

Specific heat capacity of building materials

Derivations of heat capacity and specific heat capacity
Heat capacity is mathematically defined as the ratio of a small amount of heat δQ added to the body, to the corresponding small increase in its temperature dT:

For thermodynamic systems with more than one physical dimension, the above definition does not give a single, unique quantity unless a particular infinitesimal path through the system's phase space has been defined (this means that one needs to know at all times where all parts of the system are, how much mass they have, and how fast they are moving). This information is used to account for different ways that heat can be stored as kinetic energy (energy of motion) and potential energy (energy stored in force fields), as an object expands or contracts. For all real systems, the path through these changes must be explicitly defined, since the value of heat capacity depends on which path from one temperature to another, is chosen. Of particular usefulness in this context are the values of heat capacity for constant volume, C_V, and constant pressure, C_P. These will be defined below.

Definition of heat capacity
The state of a simple compressible body with fixed mass is described by two thermodynamic parameters such as temperature T and pressure p. Therefore as mentioned above, one may distinguish between heat capacity at constant volume, C_V, and heat capacity at constant pressure, C_p:


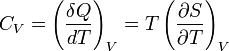
where
δQ is the infinitesimal amount of heat added,
dT is the subsequent rise in temperature.
The increment of internal energy is the heat added and the work added:

So the heat capacity at constant volume is

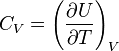
The enthalpy is defined by H = U + PV. The increment of enthalpy is

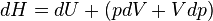
which, after replacing dU with the equation above and cancelling the PdV terms reduces to:

So the heat capacity at constant pressure is

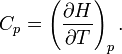
Note that this last "definition" is a bit circular, since the concept of "enthalpy" itself was invented to be a measure of heat absorbed or produced at constant pressures (the conditions in which chemists usually work). As such, enthalpy merely accounts for the extra heat which is produced or absorbed by pressure-volume work at constant pressure. Thus, it is not surprising that constant-pressure heat capacities may be defined in terms of enthalpy, since "enthalpy" was defined in the first place to make this so.

Heat capacity of compressible bodies
The specific heat capacity of a material is

which in the absence of phase transitions is equivalent to

where
C is the heat capacity of a body made of the material in question,
m is the mass of the body,
V is the volume of the body, and
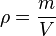is the density of the material.
For gases, and also for other materials under high pressures, there is need to distinguish between different boundary conditions for the processes under consideration (since values differ significantly between different conditions). Typical processes for which a heat capacity may be defined include isobaric (constant pressure, dp = 0) or isochoric (constant volume, dV = 0) processes. The corresponding specific heat capacities are expressed as


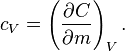
A related parameter to c is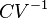 , the volumetric heat capacity. In engineering practice, for solids or liquids often signifies a volumetric heat capacity, rather than a constant-volume one. In such cases, the mass-specific heat capacity (specific heat) is often explicitly written with the subscript m, as 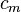. Of course, from the above relationships, for solids one writes


Specific heat capacity
The dimensionless heat capacity of a material is

where
C is the heat capacity of a body made of the material in question (J·K)
Again, SI units shown for example.

Dimensionless heat capacity

Theoretical models
The specific heat of the gas is best conceptualized in terms of the degrees of freedom of an individual molecule. The different degrees of freedom correspond to the different ways in which the molecule may store energy. The molecule may store energy in its translational motion according to the familiar formula

where m  is the mass of the molecule and [v_x,v_y,v_z] is velocity of the center of mass of the molecule. Each direction of motion constitutes a degree of freedom, so that there are three translational degrees of freedom.
In addition, a molecule may have rotational motion. The kinetic energy of rotational motion is generally expressed as

where I  is the moment of inertia tensor of the molecule, and [ω₁,ω₂,ω₃] is the angular velocity pseudovector (in a coordinate system aligned with the principle axes of the molecule). In general, then, there will be three additional degrees of freedom corresponding to the rotational motion of the molecule, (For linear molecules one of the inertia tensor terms vanishes and there are only two rotational degrees of freedom). The degrees of freedom corresponding to translations and rotations are called the "rigid" degrees of freedom, since they do not involve any deformation of the molecule.
The motions of the atoms in a molecule which are not part of its gross translational motion or rotation may be classified as vibrational motions. It can be shown that if there are n atoms in the molecule, there will be as many as 3n − 3 − n_r  vibrational degrees of freedom, where n_r is the number of rotational degrees of freedom. The actual number may be less due to various symmetries.
If the molecule could be entirely described using classical mechanics, then we could use the theorem of equipartition of energy to predict that each degree of freedom would have an average energy in the amount of (1/2)kT  where k  is Boltzmann's constant and T  is the temperature. Our calculation of the heat content would be straightforward. Each molecule would be holding, on average, an energy of (f/2)kT  where f  is the total number of degrees of freedom in the molecule. The total internal energy of the gas would be (f/2)NkT  where N  is the total number of molecules. The heat capacity (at constant volume) would then be a constant (f/2)Nk , the specific heat capacity would be (f/2)k  and the dimensionless heat capacity would be just f/2.
The various degrees of freedom cannot generally be considered to obey classical mechanics. Classically, the energy residing in each degree of freedom is assumed to be continuous - it can take on any positive value, depending on the temperature. In reality, the amount of energy that may reside in a particular degree of freedom is quantized: It may only be increased and decreased in finite amounts. A good estimate of the size of this minimum amount is the energy of the first excited state of that degree of freedom above its ground state. For example, the first vibrational state of the HCl molecule has an energy of about 5.74 × 10 joule. If this amount of energy were deposited in a classical degree of freedom, it would correspond to a temperature of about 4156 K.
If the temperature of the substance is so low that the equipartition energy of (1/2)kT  is much smaller than this excitation energy, then there will be little or no energy in this degree of freedom. This degree of freedom is then said to be "frozen out". As mentioned above, the temperature corresponding to the first excited vibrational state of HCl is about 4156 K. For temperatures well below this value, the vibrational degrees of freedom of the HCL molecule will be frozen out. They will contain little energy and will not contribute to the heat content of the HCl gas.
It can be seen that for each degree of freedom there is a critical temperature at which the degree of freedom "unfreezes" and begins to accept energy in a classical way. In the case of translational degrees of freedom, this temperature is that temperature at which the thermal wavelength of the molecules is roughly equal to the size of the container. For a container of macroscopic size (e.g. 10 cm) this temperature is extremely small and has no significance, since the gas will certainly liquify or freeze before this low temperature is reached. For any real gas we may consider translational degrees of freedom to always be classical and contain an average energy of (3/2)kT  per molecule.
The rotational degrees of freedom are the next to "unfreeze". In a diatomic gas, for example, the critical temperature for this transition is usually a few tens of kelvins. Finally, the vibrational degrees of freedom are generally the last to unfreeze. As an example, for diatomic gases, the critical temperature for the vibrational motion is usually a few thousands of kelvins.
It should be noted that it has been assumed that atoms have no rotational or internal degrees of freedom. This is in fact untrue. For example, atomic electrons can exist in excited states and even the atomic nucleus can have excited states as well. Each of these internal degrees of freedom are assumed to be frozen out due to their relatively high excitation energy. Nevertheless, for sufficiently high temperatures, these degrees of freedom cannot be ignored.

Gas phase
In the case of a monatomic gas such as helium under constant volume, if it assumed that no electronic or nuclear quantum excitations occur, each atom in the gas has only 3 degrees of freedom, all of a translational type. No energy dependence is associated with the degrees of freedom which define the position of the atoms. While, in fact, the degrees of freedom corresponding to the momenta of the atoms are quadratic, and thus contribute to the heat capacity. There are N atoms, each of which has 3 components of momentum, which leads to 3N total degrees of freedom. This gives:


where
C_V is the heat capacity at constant volume of the gas
C_V,m is the molar heat capacity at constant volume of the gas
N is the total number of atoms present in the container
n is the number of moles of atoms present in the container (n is the ratio of N and Avogadro's number)
R is the ideal gas constant, (8.314570[70] J K). R is equal to the product of Boltzmann's constant k_B and Avogadro's number
The following table shows experimental molar constant volume heat capacity measurements taken for each noble monatomic gas (at 1 atm and 25 °C):
It is apparent from the table that the experimental heat capacities of the monatomic noble gases agrees with this simple application of statistical mechanics to a very high degree.

Monatomic gas
In the somewhat more complex case of an ideal gas of diatomic molecules, the presence of internal degrees of freedom are apparent. In addition to the three translational degrees of freedom, there are rotational and vibrational degrees of freedom. In general, the number of degrees of freedom, f, in a molecule with n_a atoms is 3n_a:

Mathematically, there are a total of three rotational degrees of freedom, one corresponding to rotation about each of the axes of three dimensional space. However, in practice we shall only consider the existence of two degrees of rotational freedom for linear molecules. This approximation is valid because the moment of inertia about the internuclear axis is vanishingly small with respect other moments of inertia in the molecule (this is due to the extremely small radii of the atomic nuclei, compared to the distance between them in a molecule). Quantum mechanically, it can be shown that the interval between successive rotational energy eigenstates is inversely proportional to the moment of inertia about that axis. Because the moment of inertia about the internuclear axis is vanishingly small relative to the other two rotational axes, the energy spacing can be considered so high that no excitations of the rotational state can possibly occur unless the temperature is extremely high. We can easily calculate the expected number of vibrational degrees of freedom (or vibrational modes). There are three degrees of translational freedom, and two degrees of rotational freedom, therefore

Each rotational and translational degree of freedom will contribute R/2 in the total molar heat capacity of the gas. Each vibrational mode will contribute R to the total molar heat capacity, however. This is because for each vibrational mode, there is a potential and kinetic energy component. Both the potential and kinetic components will contribute R/2 to the total molar heat capacity of the gas. Therefore, we expect that a diatomic molecule would have a molar constant-volume heat capacity of

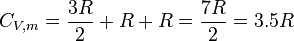
where the terms originate from the translational, rotational, and vibrational degrees of freedom, respectively.
The following is a table of some molar constant-volume heat capacities of various diatomic gasses
From the above table, clearly there is a problem with the above theory. All of the diatomics examined have heat capacities that are lower than those predicted by the Equipartition Theorem, except Br₂. However, as the atoms composing the molecules become heavier, the heat capacities move closer to their expected values. One of the reasons for this phenomenon is the quantization of vibrational, and to a lesser extent, rotational states. In fact, if it is assumed that the molecules remain in their lowest energy vibrational state because the inter-level energy spacings are large, the predicted molar constant volume heat capacity for a diatomic molecule becomes

which is a fairly close approximation of the heat capacities of the lighter molecules in the above table. If the quantum harmonic oscillator approximation is made, it turns out that the quantum vibrational energy level spacings are actually inversely proportional to the square root of the reduced mass of the atoms composing the diatomic molecule. Therefore, in the case of the heavier diatomic molecules, the quantum vibrational energy level spacings become finer, which allows more excitations into higher vibrational levels at a fixed temperature.

Diatomic gas
For matter in a crystalline solid phase, the Dulong-Petit law, which was discovered empirically, states that the dimensionless specific heat capacity assumes the value 3R. Indeed, for solid metallic chemical elements at room temperature, heat capacities range from about 2.8 to 3.4 (beryllium being a notable exception at 2.0).
The theoretical maximum heat capacity for larger and larger multi-atomic gases at higher temperatures, also approaches the Dulong-Petit limit of 3R, so long as this is calculated per mole of atoms, not molecules. The reason is that gases with very large molecules, in theory have almost the same high-temperature heat capacity as solids, lacking only the (small) heat capacity contribution that comes from potential energy that cannot be stored between separate molecules in a gas.
The Dulong-Petit "limit" results from the equipartition theorem, and as such is only valid in the classical limit of a microstate continuum, which is a high temperature limit. For light and non-metallic elements, as well as most of the common molecular solids based on carbon compounds at standard ambient temperature, quantum effects may also play an important role, as they do in multi-atomic gases. These effects usually combine to give heat capacities lower than 3 R per mole of atoms in the solid, although heat capacities calculated per mole of molecules in molecular solids may be more than 3 R. For example, the heat capacity of water ice at the melting point is about 4.6 R per mole of molecules, but only 1.5 R per mole of atoms. The lower number results from the "freezing out" of possible vibration modes for light atoms at suitably low temperatures, just as in many gases. These effects are seen in solids more often than liquids: for example the heat capacity of liquid water is again close to the theoretical 3 R per mole of atoms of the Dulong-Petit theoretical maximum.
For a more modern and precise analysis of the heat capacities of solids, especially at low temperatures, it is useful to use the idea of phonons. See Debye model.

Heat capacity at absolute zero

Heat
Heat capacity ratio
Heat equation
Heat transfer coefficient
Latent heat
Specific melting heat
Specific heat of vaporization
Temperature
Thermodynamic (absolute) temperature
Volumetric heat capacity